cliccare sull'immagine per ingrandirla

home

esposizione

scheda sintetica

approfondimenti

[La Figura 1 illustra schematicamente la struttura ed il principio di funzionamento della meridiana.
Manca la fig. 1. In essa si definisce con L il raggio della volta cilindrica e con H l'altezza delle pareti che la sostengono.
Figura 1]

Nell'arco di una giornata il Sole si muove lungo un arco di circonferenza sulla volta celeste. Esso sorge approssimativamente a Est; si fa più alto sull'orizzonte mentre si muove verso il Sud; a mezzogiorno lo si trova nella direzione Sud nella quale raggiunge la sua massima altezza sull'orizzonte; comincia quindi a calare spostandosi verso Ovest dove infine va approssimativamente a tramontare. Questo movimento è osservabile quotidianamente, con modalità che però dipendono dalle coordinate geografiche del sito di osservazione e che variano a seconda del periodo dell'anno
Come si vede in Fig. 1 l'asse della volta cilindrica punta nella direzione Nord-Sud. Questa circostanza fa sì che dall'alba a mezzogiorno il Sole illumini la parete Est della meridiana, da mezzogiorno al tramonto sarà invece illuminata la parete Ovest.
Eseguendo dei piccoli fori alla base delle due pareti (indicati in Fig. 1 con A e B) e ponendo degli specchietti orizzontalmente alla base dei fori stessi, è possibile illuminare l'interno della meridiana con un sottile pennello di luce. Il pennello di luce intercetterà la volta cilindrica in un punto dove si potrà osservare una macchia di luce. La posizione della macchia dipende ovviamente dalla posizione del Sole nel cielo e quindi dal momento del giorno nonché dal giorno dell'anno.
Risulta ora chiaro come sia possibile, dopo aver, per così dire, tarato lo strumento, adoperare la volta cilindrica come un orologio solare.

Risoluzione del problema teorico

Sotto opportune ipotesi è possibile prevedere teoricamente come la macchia di luce si muove sulla volta cilindrica. In particolare è interessante capire quali curve la macchia descrive: fissato il giorno allo scorrere delle ore; fissata l'ora al passare dei giorni.
Le ipotesi che si fanno sono fondamentalmente due: il Sole viaggia sull'eclittica con velocità angolare costante (questo equivale a considerare circolare l'orbita terrestre); è trascurabile la variazione della declinazione solare su intervalli di tempo dell'ordine di un giorno.
I calcoli, laboriosi ma non difficili, portano ai risultati che sono illustrati nelle seguenti figure.
La volta cilindrica si è immaginata sita ad una latitudine geografica F = 45°. Vicino al polo Nord o all'equatore le figure si presenterebbero in maniera sensibilmente diversa.
Si è scelto di porre H=L. E' importante sottolineare che l'operatività dell'orologio solare ( intesa come intervallo di tempo durante il quale è possibile di giorno in giorno leggere l'ora) dipende strettamente dal rapporto H/L.

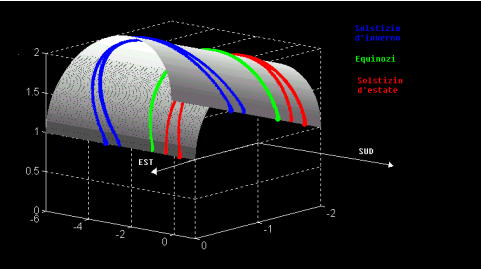
Figura 2. Nei due giorni degli equinozi la traiettoria antimeridiana e quella pomeridiana della macchia di luce si sovrappongono perfettamente.

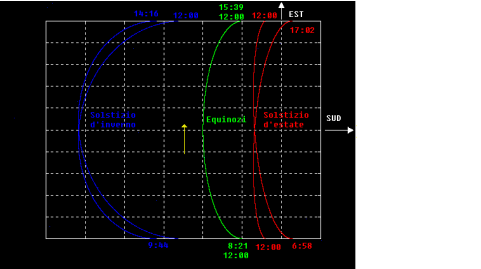
Figura 3. Questo grafico rappresenta la proiezione su un piano orizzontale della Fig.2. La freccia gialla indica il verso di percorrenza delle traiettorie. Sono anche indicati gli orari di "ingresso" e di "uscita" della macchia di luce dalla volta.

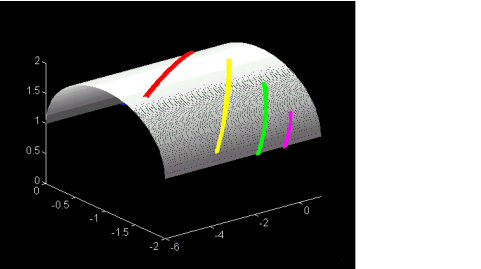
Figura 4. Sono tracciate sulla volta cilindrica le linee delle ore per t=8,9,10,11 e 12. Si noti che le linee delle 8 e delle 9 sono incomplete, nel senso che non è possibile in tutti i giorni dell'anno leggere sulla volta queste ore.

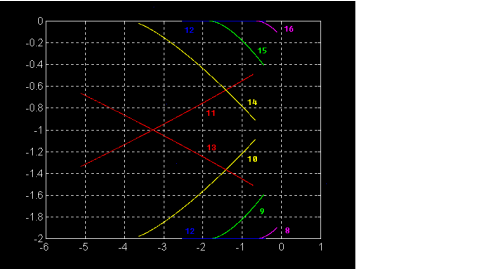
Figura 5. Questo grafico rappresenta la proiezione su un piano orizzontale della Fig. 4. Si sono in più aggiunte le linee delle ore pomeridiane, simmetriche rispetto a mezzogiorno delle ore antimeridiane.